
インド式掛け算って言うのがあるんだね。私も知らなかったんだけど、ちょっと掛け算に興味が持てるものみたい。
自分なりにちょっとやってみたから紹介するよ。
計算が早い事はやっぱりメリット

数字の計算が早い事は、大人になってからもメリットとなります。
小学生のうちではテストが早く終わるくらいしかメリットが無いのかもしれませんが、中学生になると、計算に時間がかかってしまうとテストが最後まで終わらなかったなんて事も起こります。
また、時間をかけてせっかく計算しても計算が間違っていては努力が水の泡になってしまいますよね。
逆に、計算が早い事は算数や数学が好きになるきっかけにもなり易いです。
その教科に興味を持ったり好きになる事が学力を上げる第一歩ですから、非常に大きな成果になることになります。
子供のうちから、正しい答えを素早く出せるようにしたいものですよね。
▼ 計算に強くなるにはこんな方法もあるよ ▼
実は線を引くだけで掛け算がすぐにできるようになる
日本では九九(9×9)までを暗記しますが、インドでは19×19までを暗記するそうです。
暗記してしまえば計算する必要はありませんが、習慣化されていない日本では難しいのも事実です。
ですから、簡単に計算できる方法を紹介したいと思います。
九九を線で表してみよう
例えば 3×4を考えてみましょう。
九九をマスターしている方なら、答えは12と直ぐに出ますよね。これを線で表してみましょう。
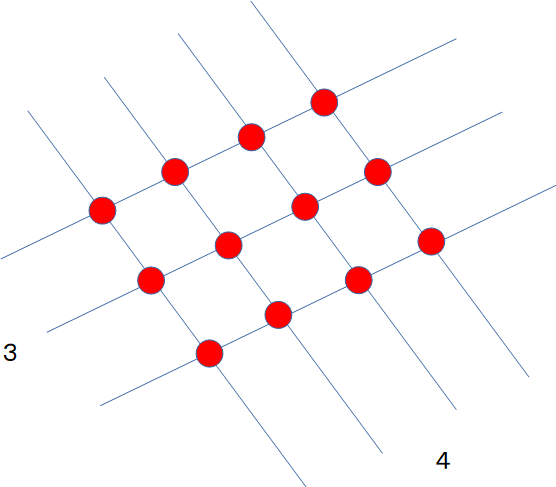
交差する線の数がそれぞれの数を表しています。
また、その解は交差する点の数で表現されます。ここでは赤い点の数で表現されていますから、赤い点が12個ある事がわかると思います。
九九の範囲では使う必要が無いと思いますが、線で掛け算を表せる事は分かってもらえると思います。

線と交点で掛け算が表現できるなんて新鮮な感じがするよね。
二桁の数字の掛け算
次に23×14を例に考えてみましょう。
暗算で解くにはちょっと難しくなってきましたかね。今回も線で解いてみる事にしましょう。
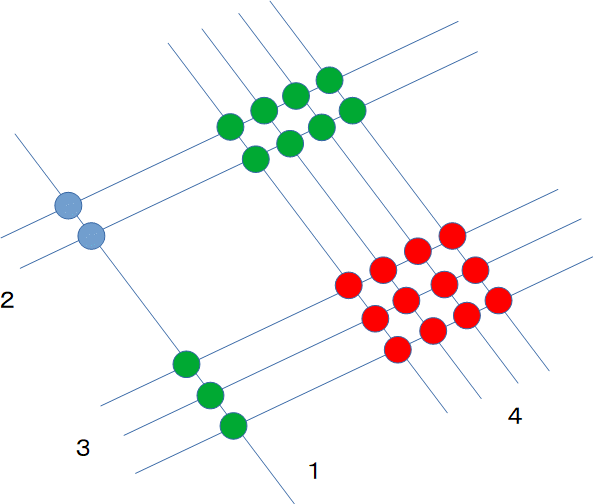
今度は10の桁と1の桁の数字に分けて線を引いて行きます。
少し斜めになるように書くと分かり易くなります。
ここでは、10の桁どうしの交点を青、10の桁と1の桁の交点を緑、1の桁どうしの交点を赤で示しています。
それぞれを足すと、青が2、緑が11、赤が12になります。
それぞれが桁数の数字を表していますので、答えは322になる事がわかると思います。
やっている事は、学校で習う計算と同じことなのですが、図で書くと興味が湧いてきませんか?

凄く不思議な感じがするけど、実際は今までの計算方法と同じなのね。
でも、凄く分かり易い気がするよ。
掛け算を面積で考えてみる
四角形の面積を計算するために掛け算を使うのは皆さんご存知ですよね。
でも、掛け算を面積で考えるのはあまりしていないのではないでしょうか。
例として16×17を考えてみましょう。図で表すとこんな感じでしょうか。
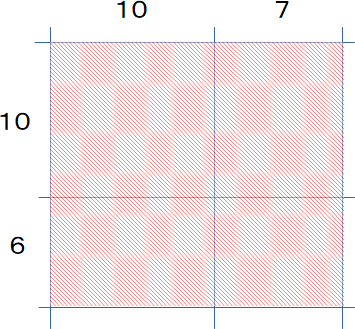
赤い網掛けのエリアの面積を計算したいのがわかりますよね。
ちょっと動かしてみましょう。
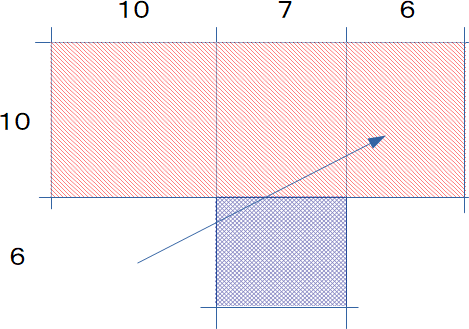
10で掛け算する部分をまとめてみました。
図では赤い網掛けの部分は10で掛け算できる部分になります。
10×(10+7+6) になりますから、230になる事がわかります。
後は残っている青い網掛け部分の面積がわかれば良いわけです。
ここは、6×7ですから九九で42と計算できます。
230+42=272になりますよね。
つまり、16×17=272です。
な~んだ当たり前じゃないかと思うかもしれませんが、ただ計算をするよりも興味が湧きませんか?
興味が湧く事が非常に大切なところなのです。

面積で表せるから、移動できるイメージが掴みやすいよね。
計算ってホントに不思議ね。
▼ 興味が出てきたら読んでみてね ▼
インド式掛け算 まとめ
今回は、インド式掛け算について紹介してみました。
自分が数学が得意じゃないので説明が上手にできないところがあったかもしれません。
しかし、実際にやってみて掛け算ってこういうものだったんだと新しい発見をしたような気持になりました。
大人でも新鮮な感じがしましたので、子供が興味を持つ可能性が十分にあると思います。
学力にとっても興味を持つことが本当に重要なことです。
算数が嫌いな子が興味を持つきっかけになったら良いですよね。



コメント