突然ですが、小学6年生の長女が「分数で割るとどうなるの?」と聞いてきました。
確かに、実際の計算方法としては理解していますが、「どうしてそうなるのか?」については説明できませんでした。
同じように小数の場合にも、計算方法はわかるのですがどうしてそうなるのか説明してあげられません。
そこで、今回は分数で割ることについてどうやって説明したら良いのか考えてみました。

私もすぐに教えられなかったので、どうやったら分かり易いか考えてみたよ。
まずは分数は割り算を表しているのを理解しよう
分数の割り算ですから、分数が理解できていないと困ります。
まずは、分数についてもう一度確認してみました。
3÷5 = 3/5
大人も子供も「そんなことわかってるよ」と言うかもしれませんが、これをしっかりと理解する事が第一歩なんです。

大人には当たり前のことなんだけど、これが分かっているのが大前提だよ。
分かっていない場合には、まずはココを重点的に教えてあげてね。
次に分数で割ってみよう
では、長女の質問である「分数で割る」ことをしてみましょう。
3 ÷ 3/5
について考えてみましょう。
大人なら、このように計算するのではないでしょうか?
3 ÷ 3/5 = 3 × 5/3 = 5
3/5を逆数にして計算するだけですから簡単に解けました。
じゃあ、なぜ逆数になるのでしょうか?
視覚的に分かり易くするように全て分数で表してみます。
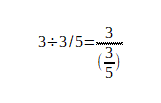
全然わかり易くなってない!と思うかもしれませんが、右項の分数の部分に注目してください。
かっこの中身を整数にしたいと思いませんか?
今回は一気に「1」にしてしまいましょう。
分数は分子と分母に同じ数を掛ければ答えは変わりませんから、5/3を両方にかけていきましょう。
先程の式に付け足していきます。
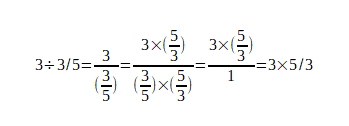
最終的に、逆数になって掛け算になっていることがわかるでしょうか?
大人の方も、計算方法はわかってもこういう意味なのか!ってなったと思います。
分数の割り算はどういう意味なのか小数の割り算で考えてみました。
分数の割り算と計算方法については、わかってもらえたと思います。
でも、「やっぱり何かしっくしり来ない」と感じる部分もありますよね。
そこで、分数を小数に置き換えて考えてみました。
【問題】
ケーキが10個あります。
これを5人で食べるとひとりいくつ食べられますか?
簡単ですよね。答えは2個です。
ちなみに、式ではこう書きましたよね。
10 ÷ 5 = 2
つまり、割る人数の一人当たりの割り当て数が計算でわかりました。
では、次の問題だったらどうでしょうか?
【問題】
ケーキが10個あります。
これを0.5人で食べるとひとりいくつ食べられますか?
「0.5人で食べる?」何言ってるの?ってなりますよね。
普通です。
ちょっと、上の下線の部分に戻ってみてください。
「割る人数の一人当たりの割り当て数」ですから、1人分の割り当てを考えるのです。
今いるのが0.5人ですから、2倍すると1人になります。
だから、答えは20(個)になりますよね。
「半分(1/2)人間がケーキ10個食べたから、1人だとすると20個分に相当するよね」と考えると少しわかった気がしませんか?

小数や分数にすると混乱しちゃうのが普通だよ。
計算の仕方さえ分かっていれば問題を解くには十分だけど、どうしてそうなるのかを理解するともっと算数が分かるようになるんじゃないかな
▼ 算数の基本は足し算だよ ▼




コメント